سری فوریه

سری فوریه یک تابع،بیان آن تابع به صورت مجموعی از جملات سینوسی و کسینوسی با آرگومان های مختلف میباشد.
از آن جا که توابع سینوسی و کسینوسی با آرگومان های خطی،متناوب هستند،لذا بدیهی است شرط لازم برای وجود سری فوریه،متناوب بودن آن تابع است.
در نظریه سریهای فوریه نشان داده شده است که اگر (f(x در شرایطی مثل (شرط دیریشله) صدق کند، میتوان آن را به صورت سری هماهنگی به شکل زیر بسط داد.
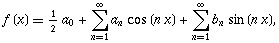
شرایط دیریکله
شرایط کافی برای وجود سری فوریه عبارتند از:
۱- انتگرال معین تابع در یک فاصله تناوب آن،همگرا باشد.
۲- تعداد نقاط ناپیوستگی تابع در یک فاصله تناوب آن محدود باشد.
۳- تعداد نقاط ماکسیمم و مینیمم (اکسترمم) تابع در یک فاصله تناوب،محدود باشد.
شرایط کافی برای وجود سری فوریه عبارتند از:
۱- انتگرال معین تابع در یک فاصله تناوب آن،همگرا باشد.
۲- تعداد نقاط ناپیوستگی تابع در یک فاصله تناوب آن محدود باشد.
۳- تعداد نقاط ماکسیمم و مینیمم (اکسترمم) تابع در یک فاصله تناوب،محدود باشد.
نام فایل: سری فوریه
مشاهده کامل مطلب: لینک به تالار گفتگو
منبع: نواندیشان
مقالات، مطالب، طرح ها و پروژه های خود را برای قرارگیری در سایت علمی آموزشی نواندیشان از اینجا بفرستید.
مطالب زیر را حتما بخوانید:
قوانین ارسال دیدگاه در سایت
- چنانچه دارای سوال فنی درباره محصول خریداری شده هستید، لطفاً از بخش حساب کاربری، تیکت ارسال کنید.
- چنانچه دیدگاهی توهین آمیز باشد و متوجه اشخاص مدیر، نویسندگان و سایر کاربران باشد تایید نخواهد شد.
- چنانچه دیدگاه شما جنبه ی تبلیغاتی داشته باشد تایید نخواهد شد.
- چنانچه در دیدگاه خود از شماره تماس، ایمیل و آیدی تلگرام استفاده کرده باشید تایید نخواهد شد.

























سلام وبتون عالیه
لطفا تبادل لینک کنید